|从圆中弦长的最值到球中截面面积的最值
文章图片

文章图片

文章图片
文章图片
看到这个标题很多人就能明白此次推送要说明的问题了 , 在二维直线与圆中这是一个必定会出现的问题 , 即过圆内一点(非圆心)的弦长的最值情况 , 若二维扩展到三维中即过球内一点(非球心)的截面圆面积的最值情况 。
这两个问题可通过类比得到 , 内容并不难理解 , 之前没有专门推送过 , 最近在整理球内的最值问题 , 在截面圆的最值问题中发现不少此类问题 , 关于球内截面圆的最值问题 , 之前有一篇推送:锥体与球体的交线以及截面圆问题 。
今天把从二维到三维的最值问题给以说明 。
一、圆内一点弦长的最值
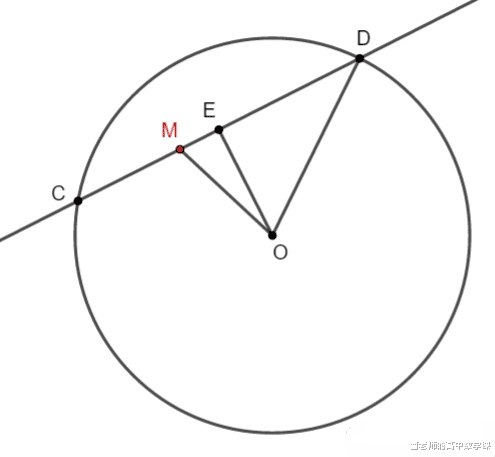
过圆内一点(非圆心)作弦长 , 弦长最大时即为圆的直径 , 这很好理解 , 当弦长最短时 , 此时圆心和该点的连线与弦长垂直 , 且该点为弦长的中点 , 这个可以通过直角三角形直角边和斜边长度的对比得出 , 如下图:
过M点的弦长CD , 取CD的中点E , 在圆的半径确定的条件下 , OE越长则弦长越短 , 直角三角形OEM中OM为斜边 , 绕弦长绕着点M运动 , 此时OE会逐渐接近OM当EM重合时OE(OM)最长 , 继续旋转 , 则OE又变回直角边 , 因此只要当CD的中点和M重合时弦长最短 , 动图如下:
关于此类问题对应的题目不再给出 , 很容易做 。
二、过球内一点截面圆面积的最值
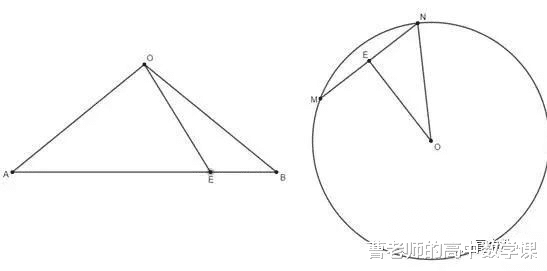
类比推理中 , 二维中的圆在三维中为球 , 二维中的线段在三维中为平面 , 过圆内一点的弦长的最值在球中对应过球内一点截面的最值 , 根据类比可猜测当截面过球心时面积最大 , 这个很好理解 , 当球心与该点的连线与截面圆垂直且该点为截面圆圆心时 , 截面圆面积最小 , 如下图:
证明过程和平面内相同 , 截面圆半径最小时 , 球心到截面圆圆心的距离最大 , 此时旋转截面 , 当球心与点M重合时两心距离最大 , 此时截面圆面积最小 , 关于立体几何中截面面积最值的题目以往常见于文科题中 , 难度不大 , 现在新高考试卷中也偶然会遇到 , 下面仅以一题为例:
之前推送的2021年太原一模理科数学中也有一个此类问题 , 结合了空间角 , 题目还不错 。
【|从圆中弦长的最值到球中截面面积的最值】下次推送将给出十一道压轴小题中与球有关的问题 。
推荐阅读
- 难处|从最难处入手 解疑难去心结
- molly|知识点17:定语从句的结构和用法(who,whom,whose)
- 考试|搞不定初级会计,会计从业资格证来了!
- |半年时间,将英语从90分提高到130分以上可能吗
- 全体师生|南京师范大学附属中学新城初级中学:科技造就未来,我们从这里启程!
- 教师|“穷人定律”不易打破,收入低的家长,普遍想让学生从事这些工作
- 杭州|继32种事业编被取消后,又有8种事业编成为公务员,教师何去何从
- 中学|你从自己的过往经历中学会了什么?
- 复旦大学|复旦教授上课时香烟从不离手,学校和学生却从不反对,为什么?
- 观点|英国Dissertation评分将从哪些方面进行考察?











