|高斯狂想曲，非常强大的高斯积分（求解技巧）

文章图片

文章图片

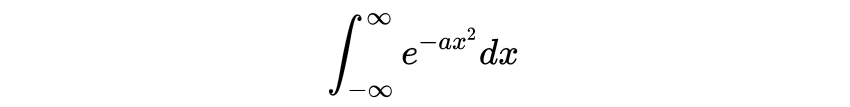
文章图片

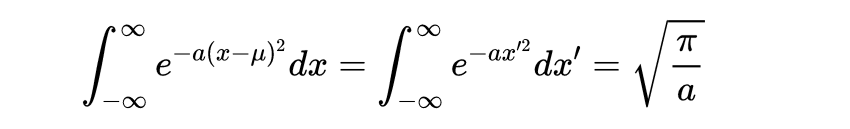
文章图片

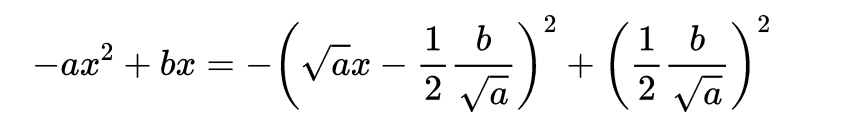
文章图片

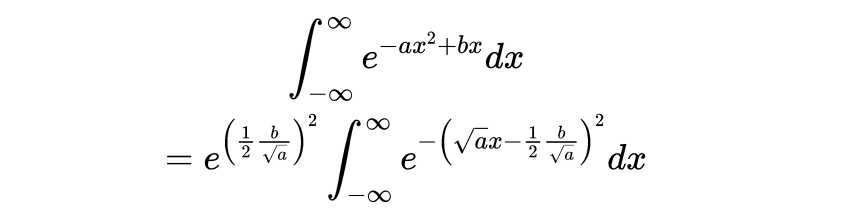
文章图片

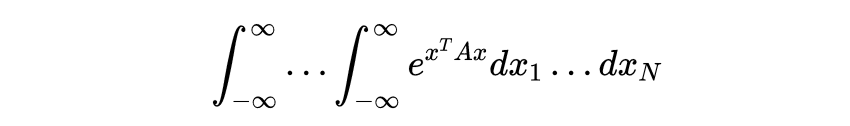
文章图片

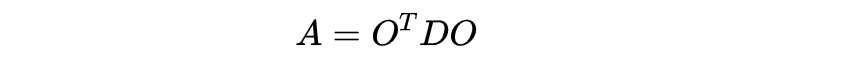
文章图片

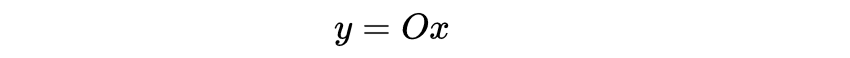
文章图片

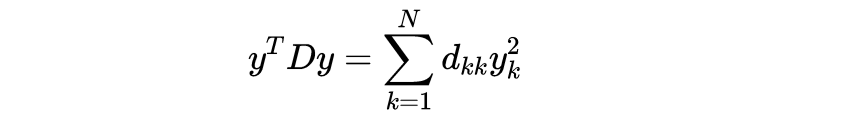
文章图片

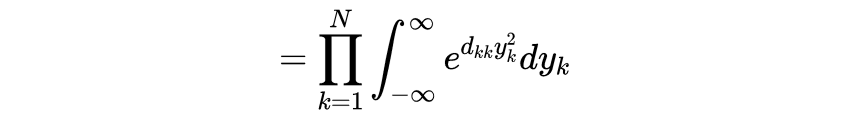
文章图片

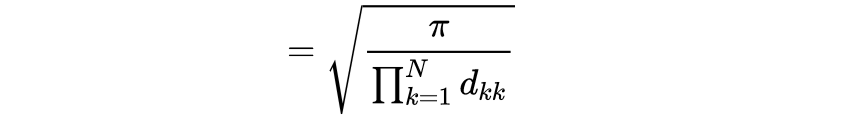
文章图片

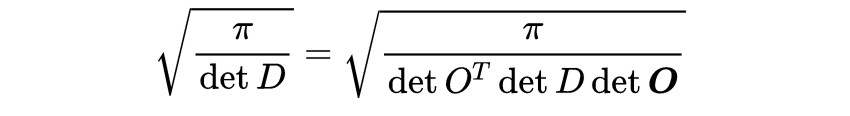
文章图片

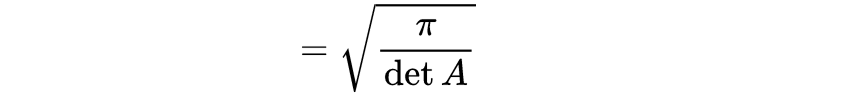
高斯积分几乎出现在数学和物理的所有领域，甚至在你意想不到的地方。高斯函数和\uD835\uDC41维中的球体的体积有密切关系。高斯积分很强大，我希望在阅读完这篇文章后，你会同意。
高斯积分是以伟大的德国数学家卡尔·弗里德里希的名字命名的

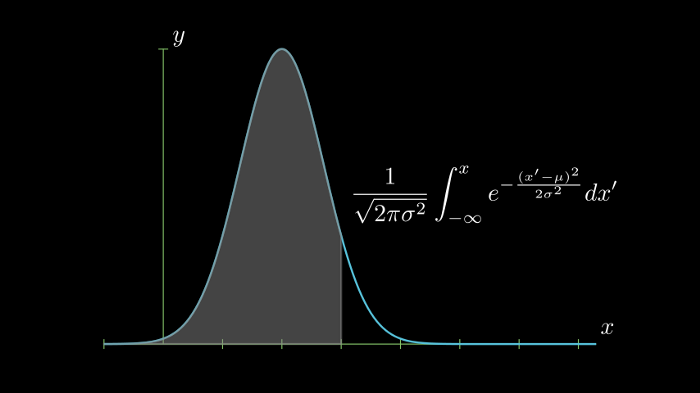
它描述了位于\uD835\uDC65=\uD835\uDF07附近的钟形曲线下的面积，下方绘制的宽度对应于\uD835\uDF0E

高斯积分是钟形高斯函数下的面积

我经常看到这个积分，但我总是记不住把这些常数放在哪里。前面的因数是2\uD835\uDF0B还是\uD835\uDF0B？\uD835\uDF0E是在平方根里面还是外面？指数是1还是1/2？
首先，让我们做一个最简单的高斯积分例子。

计算\uD835\uDC3C的诀窍是先计算\uD835\uDC3C2 ，然后取平方根。解出来后，就很容易计算

只需要做替换\uD835\uDC65→\uD835\uDC4E\uD835\uDC65 ，重复使用更简单的积分，

同样，我们得到

代换\uD835\uDC65→\uD835\uDC65?\uD835\uDF07 。只是稍微复杂一点的是

要做到这一点，只需计算

重新使用上面计算的积分：

同时，我们现在知道了高斯函数的傅里叶变换。只需替换前面结果中的\uD835\uDC4F→\uD835\uDC56\uD835\uDC4F 。几乎不经过计算，但经过论证，就得到了广义多维版本

\uD835\uDC34是一些（正）对称\uD835\uDC41×\uD835\uDC41矩阵（不一定对角线）和\uD835\uDC65是列向量