|如何利用“对数微分”简化求微过程？

文章图片

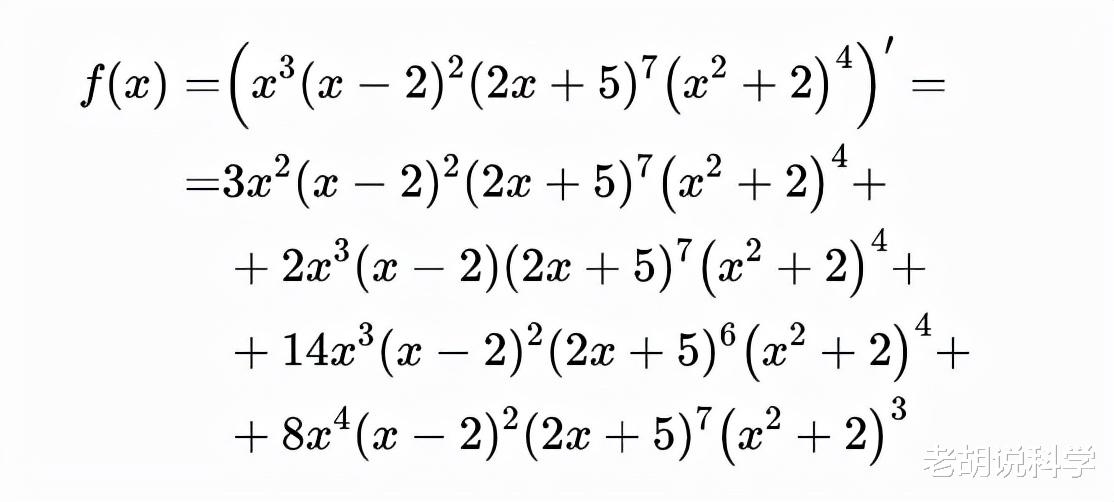
文章图片

文章图片

文章图片

文章图片

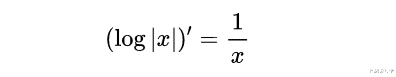
文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

一般来说，对一元函数微分是比较容易的（可导与可微等价， dy=f'(x)dx），特别是与它的分析对应物（积分）相比。在一些情况下，我们希望事情简单一些。例如，考虑以下函数：
这只不过是一个简单的实数多项式。然而，当涉及到微分时，它就不再那么简单了。乍一看，有（至少）两种微分（求导）方法。

将括号里的内容展开，然后对每一项微分
使用乘积的微分法则。

显然，第一种方法不是一个很好的选择（太繁琐）。就使用乘积的微分法则而言，情况要好一些，但仍然不够简便：
在上述情况下， f的所有因子都是多项式，但如果我们有一个像下面这样的函数，会怎么样呢：
对数微分（Log-Differentiation）那么，对于像g(x)这样复杂的情况该怎么办，因为使用通常的乘积微分法则会花费大量的时间。
我们可能还记得老师以前讲过，对数使运算更容易，因为指数变成了乘法，乘法变成了加法等等。我们可以通过取对数使这类函数的微分变得更加容易。
例如，考虑一个像下面这样的函数f：
假设上述乘积中出现的所有因子都是可微的，也是正的。那么f是正的，所以g是有意义的，其中g是以下函数：
现在，请牢记：
很容易得到下面的函数：
另一方面，观察一下：
可以得到：
因此，我们得到了一个很好的f的求导公式。虽然在计算中大量使用了对数，但得到的公式却没有对数，这主要是由于对数的导数本身并不包括任何对数，除了f中可能出现的对数。
推广在上面我们假设f的所有因子都是正的。然而，这并不是上述结果成立的必要条件。事实上，请看下面等式：
将上述内容与链式法则结合起来，我们得到以下结果：
因此，对于任何可微调且不为零的函数f ，上式也是成立的。就是说：
所以，上述公式适用于任何可微调且取非零值的函数。但是，对于有零值的函数又是怎样的呢？例如，假设f是一个这样的函数：