浙江龙网

  1. 首页 > 生活百科 > >

垂线|初二数学上册几何专项复习，辅助线是解题的关键

几何常见辅助线口诀
三角形
图中有角平分线 ， 可向两边作垂线 。
也可将图对折看 ， 对称以后关系现 。
角平分线平行线 ， 等腰三角形来添 。
角平分线加垂线 ， 三线合一试试看 。
线段垂直平分线 ， 常向两端把线连 。
线段和差及倍半 ， 延长缩短可试验 。
线段和差不等式 ， 移到同一三角去 。
三角形中两中点 ， 连接则成中位线 。
三角形中有中线 ， 倍长中线得全等 。
四边形
平行四边形出现 ， 对称中心等分点 。
梯形问题巧转换 ， 变为三角或平四 。
平移腰 ， 移对角 ， 两腰延长作出高 。
如果出现腰中点 ， 细心连上中位线 。
上述方法不奏效 ， 过腰中点全等造 。
证相似 ， 比线段 ， 添线平行成习惯 。
等积式子比例换 ， 寻找线段很关键 。
直接证明有困难 ， 等量代换少麻烦 。
斜边上面作高线 ， 比例中项一大片 。
圆
半径与弦长计算 ， 弦心距来中间站 。
圆上若有一切线 ， 切点圆心半径联 。
切线长度的计算 ， 勾股定理最方便 。
要想证明是切线 ， 半径垂线仔细辨 。
是直径 ， 成半圆 ， 想成直角径连弦 。
弧有中点圆心连 ， 垂径定理要记全 。
圆周角边两条弦 ， 直径和弦端点连 。
弦切角边切线弦 ， 同弧对角等找完 。
要想作个外接圆 ， 各边作出中垂线 。
还要作个内接圆 ， 内角平分线梦圆 。
如果遇到相交圆 ， 不要忘作公共弦 。
内外相切的两圆 ， 经过切点公切线 。
若是添上连心线 ， 切点肯定在上面 。
要作等角添个圆 ， 证明题目少困难 。
由角平分线想到的辅助线
一、截取构全等
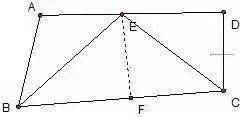
【垂线|初二数学上册几何专项复习，辅助线是解题的关键】如图 ， AB//CD ， BE平分∠ABC ， CE平分∠BCD ， 点E在AD上 ， 求证：BC=AB+CD 。

垂线|初二数学上册几何专项复习，辅助线是解题的关键
文章图片

分析：在此题中可在长线段BC上截取BF=AB ， 再证明CF=CD ， 从而达到证明的目的 。 这里面用到了角平分线来构造全等三角形 。 另外一个全等自已证明 。 此题的证明也可以延长BE与CD的延长线交于一点来证明 。 自已试一试 。
二、角分线上点向两边作垂线构全等
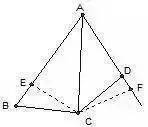
如图 ， 已知AB>AD, ∠BAC=∠FAC,CD=BC 。 求证：∠ADC+∠B=180

垂线|初二数学上册几何专项复习，辅助线是解题的关键
文章图片

分析：可由C向∠BAD的两边作垂线 。 近而证∠ADC与∠B之和为平角 。
三、三线合一构造等腰三角形
如图 ， AB=AC ， ∠BAC=90， AD为∠ABC的平分线 ， CE⊥BE.求证：BD=2CE 。
分析：延长此垂线与另外一边相交 ， 得到等腰三角形 ， 随后全等 。
四、角平分线+平行线
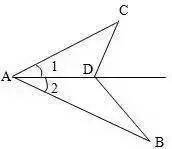
如图 ， AB>AC, ∠1=∠2 ， 求证：AB－AC>BD－CD 。

垂线|初二数学上册几何专项复习，辅助线是解题的关键
文章图片

分析：AB上取E使AC=AE ， 通过全等和组成三角形边边边的关系可证 。
由线段和差想到的辅助线
截长补短法
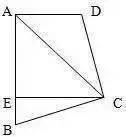
AC平分∠BAD ， CE⊥AB ， 且∠B+∠D=180° ， 求证：AE=AD+BE 。

垂线|初二数学上册几何专项复习，辅助线是解题的关键
文章图片

分析：过C点作AD垂线 ， 得到全等即可 。
由中点想到的辅助线
一、中线把三角形面积等分
如图 ， ΔABC中 ， AD是中线 ， 延长AD到E ， 使DE=AD ， DF是ΔDCE的中线 。 已知ΔABC的面积为2 ， 求：ΔCDF的面积 。

推荐阅读


上一篇：世界大学联盟|985大学发起，成立一个世界大学联盟

下一篇：year|初一英语上册必考之单词填空，练会100道考试so easy