初中数学|初中数学：铅垂高法推导及其在二次函数求面积中的巧妙应用初中数学

文章图片

文章图片

文章图片

一、什么是铅锤高法？
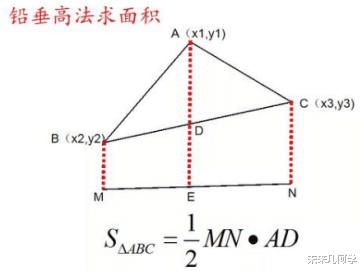
过△ABC的三个顶点分别作与水平线垂直的三条直线，垂足为M、E、N 。 MN的长度就叫做△ABC的“水平宽” ，中间的这条垂线AE在△ABC内部线段的长度AD就△ABC的“铅垂高(h)” ，我们可得出一种计算三角形面积的另一种方法：S△ABC＝1/2MN*AD ，即三角形ABC面积等于水平宽与铅垂高乘积的一半。
一、用等积法推导铅垂高法
证明：如图， AD把△ABC分成两部分△ABD、△ADC
若以AD为底，则ME、NE分别为△ABD、△ADC的高
S△ABC=S△ABD+S△ADC
=1/2ME*AD +1/2EN*AD
=1/2MN*AD
【初中数学|初中数学：铅垂高法推导及其在二次函数求面积中的巧妙应用】即三角形ABC面积等于水平宽与铅垂高乘积的一半
二、铅锤高法在二次函数求面积中的巧妙应用
注意：在二次函数中，应用铅锤高法，通常把“水平宽”映射在x轴上，少数情况也映射在y轴上。
数学成绩
例1、已知：如图，二次y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为（-10），点C(05) ，另抛物线经过点(18) ， M为它的顶点.
（1）求抛物线的解析式；
（2）解：过点M作MN∥y轴交BC轴于点N ，则△MCB的面积=△MCN的面积+△MNB的面积= MN?OB÷2.
∵y=-x2+4x+5=-（x-5）（x+1）=-（x-2）2+9 ，
∴M（2 ， 9）， B（5 ， 0），
由B、C两点的坐标易求得直线BC的解析式为：y=-x+5 ，
当x=2时， y=-2+5=3 ，则N（2 ， 3），
则MN=9-3=6 ，
则S△MCB=MN*OB/2 =6×5÷2=15.（铅垂高法）
如果用一般的割补法：S△MCB=S△MEB+S梯形MCOE-S△MCB ，那么计算量会很大
下面我们再来看一道例题：
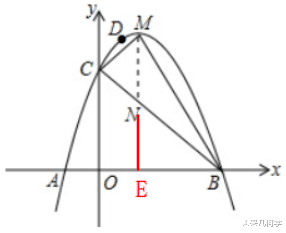
例2、如图1 ，抛物线y＝－x2＋bx＋c与x轴交于A(1 ， 0) ， B(－3 ， 0)两点。
(1)求该抛物线的解析式；
(2)设(1)中的抛物线交y轴于C点，在该抛物线的对称轴上是否存在点Q ，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由；
(3)如图2 ，在(1)中的抛物线上的第二象限上是否存在一点P ，使△PBC的面积最大？若存在，求出点P的坐标及△PBC的面积最大值；若没有，请说明理由。
解：(1)抛物线解析式为y＝－x2－2x＋3；
（2）Q(－1 ， 2)；
（3）如图6 ，作PE⊥x轴于点E ，交BC于点F．
设P点（x ，－x2－2x＋3）（－3<x<0）．
由例题1和2 ，您是不是发现掌握了铅垂高法，在二次函数中求面积就会变得异常简单呢？

初中数学|初中数学：铅垂高法推导及其在二次函数求面积中的巧妙应用

推荐阅读

农村户口无房市区有两套房孩子读书按哪一套

广东2023年高考怎么考 2023广东高考考前提醒

水不能反复烧开,为什么水为什么不能反复烧开水反复烧开后会怎样

信用卡欠款不还有什么后果信用卡欠款不还怎么办

锡纸可以放电磁炉上加热吗?，铝箔餐盒可以放电磁炉上使用吗？

2023年百里杜鹃景区每日开园时间今年百里杜鹃的门票是多少

紫金山昆虫博物馆地铁能直达吗南京紫金山昆虫博物馆交通指南

水遁水龙弹之术结印水遁水龙弹之术结印慢动作

山药披萨的做法山药披萨怎么做

影之刃3魔弦攻略,魔弦装备及技能搭配详解,新发布的哦

“出大事了，一对父女死了”，竟是因为这个！你家就有！

2023太原古县城徒步赛报名最新消息太原古县城自驾游玩攻略

阿组词阿组词1000个

2023瑞安市医疗服务集团赴高校招聘硕士及以上研究生体检工作公告

金毛狗冬天在外面睡觉会冷吗

电脑需要托运还是随身携带

英语食物类单词 20个有关食物的英语单词？？

炖乌鸡都需要放什么调料炖乌鸡需要放什么配料

去黑头最有效的方法是什么如何去黑头

苹果手机关机后一直白苹果怎么办（白苹果了怎么强制关机)