fx|微积分的基本思想，三重积分在现实生活中的作用微积分

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

为什么我们在现实生活中会需要三重积分。我们要把它分解开来。我们先来分析一下，为什么我们需要积分，然后是二重积分，最后是三重积分。
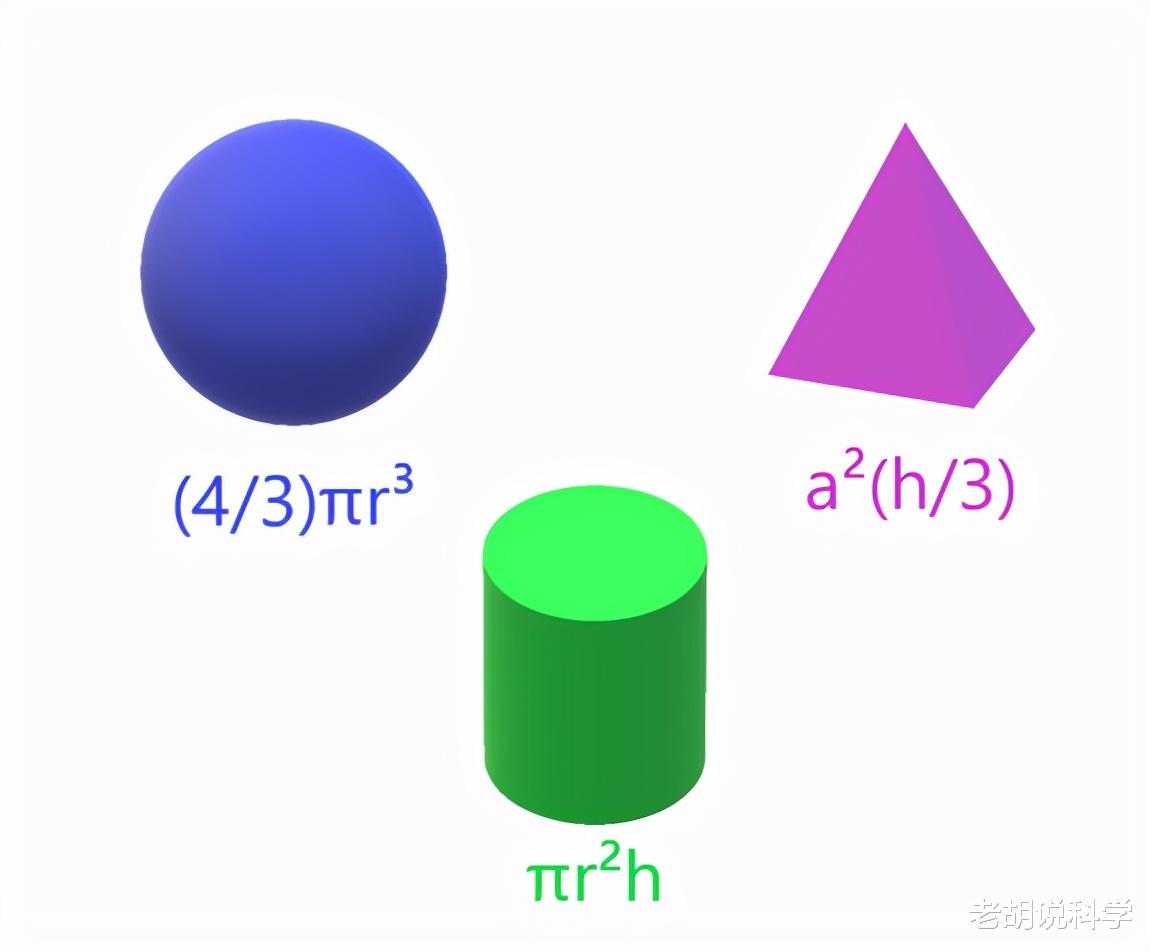
如何理解积分对于简单的图形，我们有现成的公式来求它们的面积。
但我们如何求下面图形的面积呢？
答案是，我们可以使用积分。描这里的积分就可以理解为曲线下面的面积。假设我们想求一条奇怪的曲线下面的面积，它看起来像这样：
用公式法求这样的面积是很困难的。我们希望用更简单的形状去近似或者代替它，比如矩形，面积公式是长乘以宽。那我们为什么不在曲线下画一堆矩形，求这些矩形的面积，然后把所有的小矩形面积加起来，来近似计算曲线下的面积，就像这样：
这是个不错的近似值，值为所有绿色矩形的面积之和。
每个矩形都有相同的宽度，以使计算更容易。宽度等于一个我们称之为Δx的量（概念上， Δx是x的变化）。每个矩形的高度是不同的，但它是由函数f(x)给出的，由图中弯曲的黑线表示。
为了体现高度是不同的，从左边开始的第一个矩形的高度是f(x?) ，第二个矩形的高度是f(x?) ，以此类推。一般来说，第i个矩形的高度为f（x?）。
矩形的面积是高度乘以宽度，所以其中一个矩形的面积等于f（x?）*Δx 。如果我们把所有的矩形面积加起来，我们就可以得到曲线下的近似面积。
但是我们的近似值并不那么精确，我们可以通过增加矩形的数量使近似值更准确，就像这样：
注意， Δx现在更小了。而且，这个和比上一个更准确。我们可以继续把图形分成越来越小的矩形，使值更加精确。最终，随着矩形的数量接近无穷大（每个矩形的宽度接近0），近似面积越来越接近实际面积。
这个总和被称为积分。积分就是这样写出来的。
积分符号∫看起来像一个大的S 。当一个叫戈特弗里德-莱布尼茨的德国人发展微积分时，他认为积分是一个无限的和。 dx \"代表Δx ，即每个矩形的宽度，它现在是无限小的。这个 \"dx \"被称为微分。

fx|微积分的基本思想，三重积分在现实生活中的作用

推荐阅读

这辈子没什么野心只求合家平安的星座？

锌对人体有什么作用锌对人体有什么作用与功效

想买台打印机，主要打印作业用，你觉得激光的好，还是喷墨的好，你有哪些推荐？

牛年王姓宝宝起名大全姓王的牛宝宝名字大合集

干鹿茸需要冷藏还是冷冻鹿茸湿的好还是干的好

班主任工作申请书

弹的多音字组词弹的多音字组词语

斑马会员怎么注销

笔记本电脑键盘进水了怎么办？抢救进水键盘攻略，拯救者笔记本电脑键盘进水了怎么办？

破水多久后会生下来

关于浙江财经大学法学院简述浙江财经大学法学院

黄酒煮鸡蛋的功效黄酒煮鸡蛋有什么功效

高考零分的蒋多多最近状况

华为荣耀8还值得买么

闲置土地处置方法闲置土地怎么处置

葛根粉和茯苓粉一起吃的功效葛根粉和茯苓粉

moto8 cn|中国最大的摩托车论坛

加你qq空间单独设置密码操作 qq空间独立密码怎么设置

银行周末能办卡吗(图文银行周末能办卡吗)

猕猴桃秋天可以移栽吗猕猴桃秋天可以移栽吗图片