初中数学|初中数学四点共圆判定方法 五道例题你能证明三道说明你有真水平
文章图片

文章图片

文章图片

文章图片

文章图片
四点共圆的判定方法有很多 , 今天 , 我们只简单
一、四点共圆五种判定方法:
1、对角互补法:若平面上四点连成四边形的对角互补或一个外角等于其内对角 , 那么这四点共圆;特殊情形——若一个四边形有两个对角都为90o , 那么该四边形四个顶点共圆;
推论:同斜边的直角三角形四点共圆 。
2、同侧共底边三角形顶角相等法:若线段同侧二点到线段两端点连线夹角相等 , 那么这二点和线段二端点四点共圆(同弧所对圆周角相等)
也可表述为:把被证共圆的四个点连成共底边的两个三角形 , 且两三角形都在这底边的同侧 , 若能证明其顶角相等 , 从而即可肯定这四点共圆 。
3、中垂线法:连成的四边形三边中垂线交于一点 , 则这四点共圆.
证明:如图ABCD是连成的四边形 其三边ABCD DA的中垂线交于点O
因为OE是AB的中垂线 所以OA=OB(线段中垂线上任何一点到线段两个端点距离相等)
【初中数学|初中数学四点共圆判定方法 五道例题你能证明三道说明你有真水平】同理 有 OA=OD OD=OC
即OA=OB=OC=OD(四个点到一定点的距离相等)
所以 A B C D四点共圆圆心即连成的四边形各边中垂线的交点.
4、相交弦定理的逆定理:把被证共圆的四点两两连成相交的两条线段 , 若能证明它们各自被交点分成的两线段之积相等 , 即可肯定这四点共圆;
5、割线定理的逆定理:或把被证共圆的四点两两连结并延长相交的两线段 , 若能证明自交点至一线段两个端点所成的两线段之积等于自交点至另一线段两端点所成的两线段之积 , 即可肯定这四点也共圆.(见例5)
二、具体方法、例题解析
2.1、对角互补法
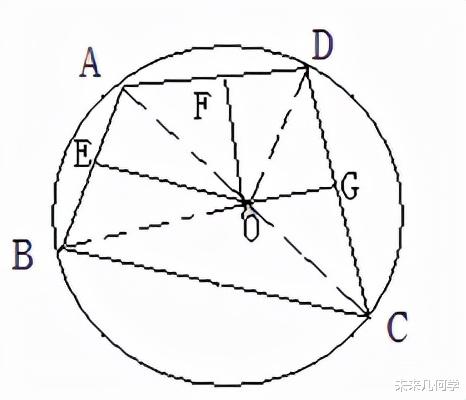
例1、已知:如图 , O 是半圆的圆心 , C、E 是圆上的两点 , CD⊥AB , EF⊥AB , EG⊥CO. 求证:CD=GF
2.2、同侧共底边三角形顶角相等法(应用较多)
例2、设 MN 是圆 O 外一直线 , 过 O 作 OA⊥MN 于 A , 自 A 引圆的两条直线 , 交圆于 B、C 及 D、E , 直线 EB 及 CD 分别交 MN 于 P、Q.
求证:AP=AQ.
证明:作 E 点关于 GA 的对称点 F , 连 FQ、FA , FC ,
∵OA⊥MN , EF⊥OA ,
则有∠FAP=∠EAQ , ∠EAP=∠FAQ , FA=EA ,
∵E , F , C , D 共圆
∴∠PAF=∠AFE=∠AEF=180°﹣∠FCD ,
∵∠PAF=180﹣∠FAQ ,
∴∠FCD=∠FAQ ,
∴FCAQ 四点共圆 ,
∠AFQ=∠ACQ=∠BED ,
在△EPA 和△FQA 中
∠PEA = ∠QFA
AF = AE
∠PAE = ∠QAF
∴△EPA≌△FQA ,
∴AP=AQ.
注:证两线段相等 , 一般考虑证所在的两三角形全等.
例3、设 P 是平行四边形 ABCD 内部的一点 , 且∠PBA=∠PDA.
求证:∠PAB=∠PCB.
方法思路: 利用平行四边形的性质构造新的平行线 , 将条件中相等但分散的角集中起来 。 过 P 点平行于 AD 的直线 , 并选一点 E , 使 PE=AD=BC , 利用 AD∥EP , AD∥BC , 进而得出 ∠ABP=∠ADP=∠AEP , 得出 AEBP 共圆 , 即可得出答案.
推荐阅读
- 数学|称平行线能相交的数学奇才,遭质疑郁郁而终,其理论12年后被证实
- 申论|初中数学|实际问题与二次函数专题讲解+例题解析+专项训练,收藏
- 教师|2022考研数学是否为历年最难?难在哪里?
- 数学|要先拿个诺贝尔奖才能申请美国EB1A?
- 留学生|掌握这16招解题方法,高中数学冲刺130+不用愁!
- 中学业|宿州市2022年初中学业水平体育与健康学科考试工作方案
- 大学|高一学生期末数学56、物理28,化学41,还有希望考重点大学吗?
- 数学|18岁一战成名,与“韦神”齐名的北大才子,数学界“颜值天花板”
- 中小学|在小学和初中,为啥同届孩子中年龄大的成绩更好?出生月份有优势
- 宿迁学院|初中生“身高标准”,很多学生未达标,家长:要重视











