|天才高斯——19世纪最伟大的数学家，近代数学的奠基者

文章图片

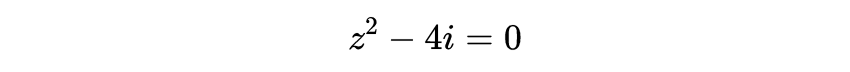
文章图片

文章图片

文章图片

文章图片

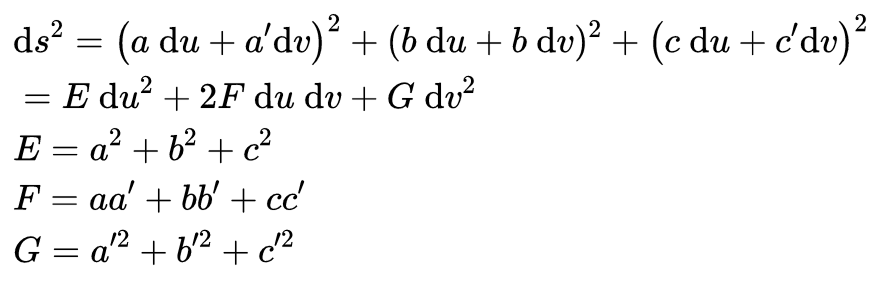
卡尔·弗里德里希·高斯（1777~1855）是一个神童。 19岁差一个月的他作出了一项非凡的发现。 2000多年以来，人们知道如何用直尺和圆规作等边三角形和正五边形（还有其他的正多边形，其边数是2、3、5的倍数），但不知道如何作出边数为素数的正多边形。高斯证明，正七边形也能用直尺和圆规作出。

【|天才高斯——19世纪最伟大的数学家，近代数学的奠基者】高斯日记

高斯通过写日记来纪念他的发现，在接下来的18年里，他在这本日记中记下了他的很多发现。他还是一个学生的时候就获得了很多成功。其中有一些是对欧拉、拉格朗日及其他18世纪数学家们已经证明的定理的重新发现；有很多是新发现。在他学生时代的更重要的发现中，我们可以挑出最小平方法、数论中二次互反律的证明，以及他对代数基本定理的研究。他获得了博士学位，学位论文的标题是《关于所有含一个变量的有理代数整函数都能分解为一次或二次实因子的定理的新证明》。这是他一生中所发表的代数基本定理的4个证明当中的第一个，在这篇论文中，高斯强调了在证明这个定理的过程中证实至少有一个根的重要性。下面的说明可以显示他的思路。
我们可用图示的方法解方程

证明存在一个复数值z=a+bi满足这个方程。用a+bi取代z ，并分开方程中的实数部分和虚数部分，我们就得到a^2-b^2=0和ab-2=0 。把a和b解释为变量，并在同一坐标系中画出这些函数，一个坐标轴代表实数部分a ，另一个坐标轴代表虚数部分b ，我们就有了两条曲线；一条由直线a+b=0和a-b=0构成，另一条由等轴双曲线ab=+2构成。

很显然，这两条曲线有一个交点P在第一象限。我们应该特别注意，第一条曲线的一条分支沿着θ=1π/4和θ=3π/4的方向离开原点；第二条曲线的一条分支渐近地向着θ=0π/4和θ=2π/4的方向移动；交点在最后两个方向θ=0和θ=π/2之间。这个交点的a和b的坐标是方程z^2-4i=0的一个解的实数部分和虚数部分。假如我们最初的多项式方程是三次而不是二次，则一条曲线的一根分支就会趋近于θ=1π/6和θ=3π/6的方向，另一条曲线就会趋近于θ=0π/6和θ=2π/6的方向。在每一种情况下这些分支都是连续的，因此，它们一定要相交于θ=0至θ=π/3之间的某个地方。
对于一个n次方程来说，一条曲线的一根分支有渐近方向θ=1π/2n和θ=3π/2n ，而另一条曲线的分支有渐近方向θ=0π/2n和θ=2π/2n 。这些分支必定相交于从θ=0至θ=π/n之间，这个交点的a和b的坐标，就是满足这个方程的复数的实数部分和虚数部分。因此我们看到，不管一个多项式方程的次数是几，它必定至少有一个复数根。我们会注意到，高斯依靠这些曲线的图示来证明它们相交。承认这个结果，多项式方程可以分解为一次或二次实因子也就得到了证明。