
文章图片
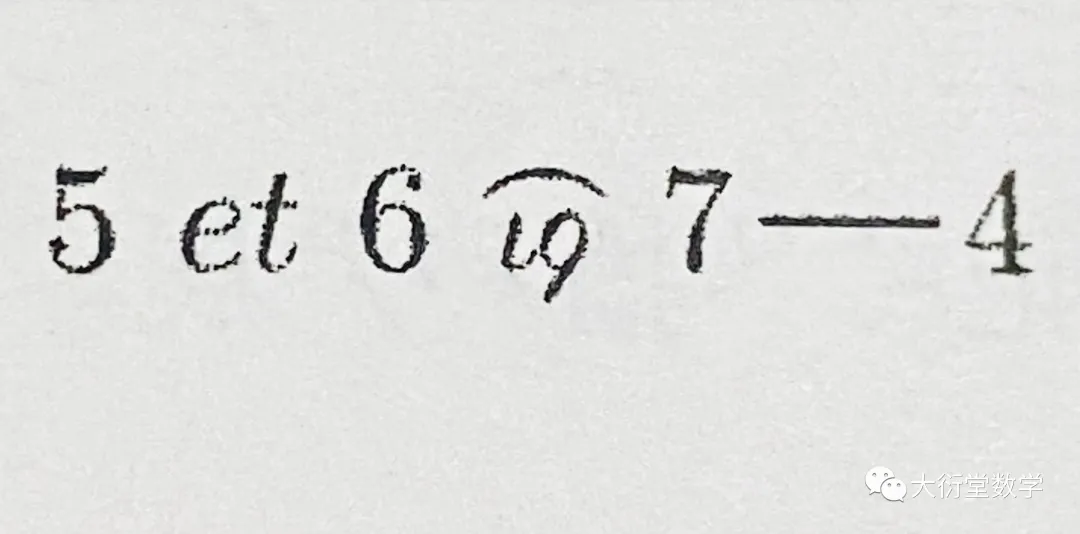
文章图片

文章图片
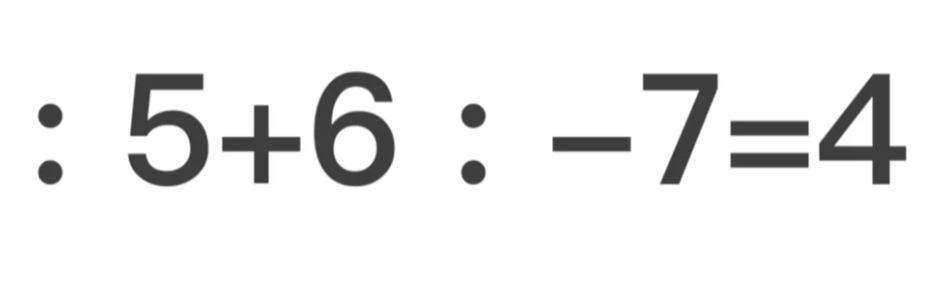
文章图片
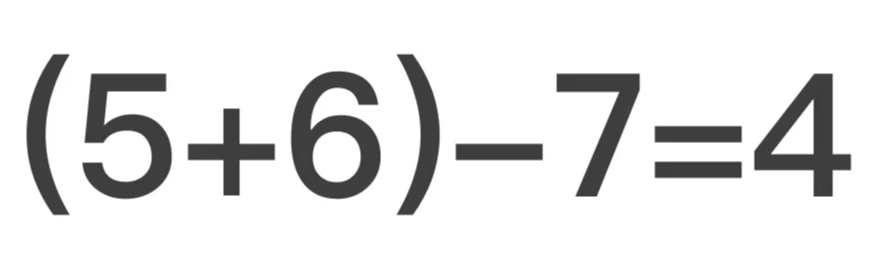
文章图片
读写算法:基本符号 ??
你会怎么运用算术符号表示“将5和6的和减去7 , 结果是4”?
或许你会这样表示:(5+6)-7=4 。
如果这样做 , 几乎所有学过初等算术的人都能理解 , 不管他们所在的国家或他们所说的语言 , 都能更清楚地读和书写 , 不会出错 。
算术符号已成为通用的符号 。 它们比任何字母系统的字母或任何语言的缩写 , 都更容易被人们普遍理解和接受 。
【面试技巧|我和数学史有个约会(四)|加减乘除的演变过程,已拿捏!】但古时并非如此 , 古希腊人和他们的阿拉伯继承人并没有使用任何符号来做算术运算或表示运算关系 , 他们用文字写出他们的问题和解答方法 。
事实上 , 许多世纪以来 , 甚至一直贯穿中世纪 , 大多数人都是用文字来书写和表示算术与代数的 。
算术符号在文艺复兴初期就以书面形式出现 , 但无论是人与人之间 , 还是国家与国家之间 , 符号几乎都是不一致的 。
随着15世纪活字印刷术的发明 , 印刷书籍开始显示出更多的一致性 。 然而 , 还是经过了漫长时间后 , 我们今天使用的符号才成为书面算术的共同组成部分 。
15世纪70年代 , 雷乔蒙塔努斯(1436-1476 , 德国数学家、天文学家)在德国就写了:
(et这个词在拉丁语中的意思是“和”)
1494年 , 另一种写法出现在卢卡·帕乔利的《算术、几何、比及比例概要》 , 即《数学大全》中 , 并广泛应用于意大利和欧洲其他地区 , 这个写法如下:
第一个数的分组可能被省略括号 , 假设它显然是首先要做的 。 式子中表示相加相减的符号在欧洲大部分地区都很流行 。
1489年 , 大约同一时间在德国 , 我们现在熟悉的加号和减号第一次出现在约翰·魏德曼的商业算术著作中 。 魏德曼没有表示等于的符号 , 所以他的版本可能有点像下面的样子:
(德语短语“das ist”的意思是“就是”)
但是 , 魏德曼也用“+”表示非算术意义“和”的缩写 , 用“-”来作为通用分离标记的缩写 。 这些符号具有的
1557年 , “+”和“-”在英语书籍中第一次使用 , 出现在罗伯特·雷科德代数课本《砺智石》 。 在这本书中雷科德将“=”作为等号的符号 。 他说的话证明了这一点 , “没有比这两条同长度的平行线更相等的了” 。 其他标志也被他拉长了 , 他
雷科德的符号并没有立即受欢迎 。 许多欧洲数学家还喜欢使用(p~)和(m~)表示加和减 , 特别是在意大利、法国、西班牙 。 半个多世纪 , 他的等号也没有出现在印刷品上 。 同时 , 符号“=”也被一些有影响力的数学家用来表示其他意思 。 例如 , 在1646年版的弗兰索瓦·韦达的文集中 , 它被用来表示两个不清楚大小的代数量相减上 。
推荐阅读
- 什么|广州入户心得:我不是学霸,只是听话照做了~
- 社会|7岁男孩“憋着不能哭”令网友破防,我们应做些什么?
- 爱心|我,70后贫困山村校长,借钱供儿子上学,却甘愿为学生自掏20多万
- 考试|0分小学生试卷走红,教师看完啼笑皆非,稻子:我也很无辜啊!
- 天性|“家教杂说”之二十八:《郭橐驼由种树谈育人》
- 高中物理|评上副高之后,优秀名额都让给别人了,教师:我也10多年不优秀了
- 理工科|专升本or就业,我来支支招!
- |“我在家也是小公主”,00后辞职信如“段子”,老板看完语塞
- 大学生|“我们不招太漂亮的女生”,名企面试官坦言,自己的判断有理有据
- 中国科学院大学|2022ESI我国院校排名更新,清北无缘榜首,华中大和武大排名下降









