A.1:1:1 B.2:2:3 C.2:3:2 D.3:2:2
【考点】角平分线的性质.21 世纪教育网
【分析】根据角平分线上的点到角的两边距离相等可得点P到△ABC三边的距离相等 , 然后根据等高的三角形的面积的比等于底边的比解答.
【真题|初二数学上册角平分线历年真题精选30道(含解析)】【解答】解:∵P为三边角平分线的交点 ,
∴点P到△ABC三边的距离相等 ,
∵AB , BC , CA的长分别为6cm , 4cm , 4cm ,
∴△ABP , △BCP , △ACP的面积比=6:4:4=3:2:2.
故选D.
【点评】本题考查了角平分线上的点到角的两边距离相等的性质 , 等高的三角形的面积的比等于底边的比 , 熟记性质并判断出点P到△ABC三边的距离相等是解题的关键.
7.(2015?江西校级模拟)如图 , 在△ABC中 , ∠C=90° , AD平分∠CAB , 已知CD=3 , BD=5 , 则下列结论中错误的是()
A.AC=6 B.AD=7 C.BC=8 D.AB=10
【考点】角平分线的性质.21 世纪教育网
【分析】过点D作DE⊥AB于点E , 由角平分线的性质可知CD=DE=3 , 由勾股定理求出BE的长 , 再由相似三角形的判定定理得出△BED∽△BCA , 故可得出AC及AB的长 , 在Rt△ACD中 , 根据勾股定理求出AD的长即可.
【解答】解:∵CD=3 , BD=5 ,
∴BC=CD+BD=3+5=8 , 故C正确;
过点D作DE⊥AB于点E ,
∵AD平分∠CAB ,
∴CD=DE=3.
在Rt△BDE中 ,
∵BD=5 , DE=3 ,
∴BE===4.
∵∠B=∠B , ∠DEB=∠C ,
∴△BED∽△BCA ,
∴== , 即== , 解得AB=10 , AC=6 , 故A , D正确;
在Rt△ACD中 ,
∵AC=6 , CD=3 ,
∴AD===3 , 故B错误.
故选B.
【点评】本题考查的是角平分线的性质 , 根据题意构造出直角三角形 , 利用勾股定理求解是解答此题的关键.
8.(2015春?成都校级期末)如图是一块三角形的草坪 , 现要在草坪上建一凉亭供大家休息 , 要使凉亭到草坪三条边的距离相等 , 凉亭的位置应选在()
A.△ABC的三条中线的交点 B.△ABC三边的中垂线的交点
C.△ABC三条高所在直线的交点 D.△ABC三条角平分线的交点
【考点】角平分线的性质;作图—应用与设计作图.21 世纪教育网
【分析】由于凉亭到草坪三条边的距离相等 , 所以根据角平分线上的点到边的距离相等 , 可知是△ABC三条角平分线的交点.由此即可确定凉亭位置.
【解答】解:∵凉亭到草坪三条边的距离相等 ,
∴凉亭选择△ABC三条角平分线的交点.
故选D.
【点评】本题主要考查的是角的平分线的性质在实际生活中的应用.主要利用了到线段的两个端点的距离相等的点在这条线段的垂直平分线上.
9.(2015秋?平南县月考)如图 , Rt△ABC , ∠C=90° , AD平分∠CAB , DE⊥AB于E , 则下列结论中不正确的是()
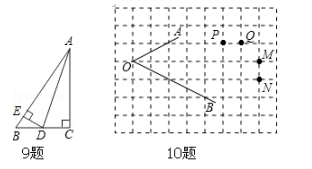
文章图片
A.BD+ED=BC B.DE平分∠ADB
C.AD平分∠EDC D.ED+AC>AD
【考点】角平分线的性质.21 世纪教育网
【分析】根据已知条件由角平分线的性质可得结论CD=DE , 由此又可得出很多结论 , 对各选项逐个验证 , 证明.
【解答】解:CD=DE ,
∴BD+DE=BD+CD=BC;
又有AD=AD ,
可证△AED≌△ACD
∴∠ADE=∠ADC
即DE平分∠ADB;
在△ACD中 , CD+AC>AD
所以ED+AC>AD.
故选B.
【点评】本题主要考查平分线的性质 , 由已知证明△AED≌△ACD是解决的关键.
推荐阅读
- 数学|称平行线能相交的数学奇才,遭质疑郁郁而终,其理论12年后被证实
- 申论|初中数学|实际问题与二次函数专题讲解+例题解析+专项训练,收藏
- 教师|2022考研数学是否为历年最难?难在哪里?
- 数学|要先拿个诺贝尔奖才能申请美国EB1A?
- 留学生|掌握这16招解题方法,高中数学冲刺130+不用愁!
- 大学|高一学生期末数学56、物理28,化学41,还有希望考重点大学吗?
- 数学|18岁一战成名,与“韦神”齐名的北大才子,数学界“颜值天花板”
- 数学|如何看待2021CPA财管复核成绩异常?
- 高校|新高考模式下,理科分数要想超过600分,决定权不在数学而是这科
- 数学|黑龙江状元放弃哈工大本硕博连读,选择复读,最后考了多少











