浙江龙网

  1. 首页 > 生活百科 > >

真题|初二数学上册角平分线历年真题精选30道（含解析）( 五 )

距离性质真题分析考查历年面积上册三角形初二角平分线平分线Rt世纪教育网


三．解答题（共10小题）
21．（2015?路南区二模）在学完全等三角形后 ， 李老师给出了下列题目：
求证：角的内部到角的两边距离相等的点在角的平分线上．
已知：
求证：
证明：

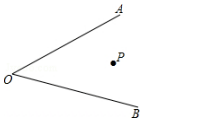
真题|初二数学上册角平分线历年真题精选30道（含解析）
文章图片

【考点】角平分线的性质．21 世纪教育网
【分析】连接OA ， 作OE⊥AC ， OF⊥AB， 垂足分别为E、F ， 将△ABC的面积分为：S△ABC=S△OBC+S△OAC+S△OAB ， 而三个小三角形的高OD=OE=OF ， 它们的底边和就是△ABC的周长 ， 可计算△ABC的面积．2-1-c-n-j-y
【解答】解：作OE⊥AC ， OF⊥AB ， 垂足分别为E、F ， 连接OA ，
∵OB ， OC分别平分∠ABC和∠ACB ， OD⊥BC ，
∴OD=OE=OF ，
∴S△ABC=S△OBC+S△OAC+S△OAB
=×OD×BC+×OE×AC+×OF×AB
=×OD×（BC+AC+AB）
=×3×21=31.5．
故填31.5．
【点评】此题主要考查角平分线的性质；利用三角形的三条角平分线交于一点 ， 将三角形面积分为三个小三角形面积求和 ， 发现并利用三个小三角形等高是正确解答本题的关键．
22．（2015春?泰山区期末）如图 ， 在△ABC中 ， ∠C=90° ， AD平分∠CAB ， 交CB于点D ， 过点D作DE⊥AB于点E．

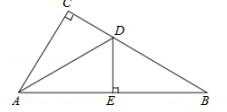
真题|初二数学上册角平分线历年真题精选30道（含解析）
文章图片

（1）求证：AC=AE；
（2）若点E为AB的中点 ， CD=4 ， 求BE的长．
【考点】 角平分线的性质；全等三角形的判定与性质． 21 世纪教育网
【分析】 根据题意画出图形 ， 写出已知和求证 ， 根据全等三角形的判定和性质证明结论．
【解答】 已知：PE=PF ， PE⊥OA于E ， PF⊥OB于F ，
求证：点P在∠AOB的平分线上．
证明：在Rt△POE和Rt△POF中 ，
，
∴Rt△POE≌△RtPOF，
∴∠EOP=∠FOP，
∴ 点P在∠AOB的平分线上．
【点评】 本题考查的是角平分线的判定的证明 ， 灵活运用直角三角形全等的判定定理是解题的关键．
23．（2015?黄岛区校级模拟）现要在三角地ABC内建一中心医院 ， 使医院到A、B两个居民小区的距离相等 ， 并且到公路AB和AC的距离也相等 ， 请确定这个中心医院的位置．

真题|初二数学上册角平分线历年真题精选30道（含解析）
文章图片

【考点】 角平分线的性质；线段垂直平分线的性质；作图—应用与设计作图． 21 世纪教育网
【分析】 根据线段垂直平分线性质作出AB的垂直平分线 ， 根据角平分线性质作出∠BAC的角平分线 ， 即可得出答案．
【解答】 解：
作AB的垂直平分线EF ， 作∠BAC的角平分线AM ， 两线交于P ，
则P为这个中心医院的位置．
【点评】 本题考查了线段垂直平分线性质 ， 角平分线性质的应用 ， 主要考查学生的理解能力和动手操作能力
24．（2015春?澧县期末）如图：在△ABC中 ， ∠C=90° AD是∠BAC的平分线 ， DE⊥AB于E ， F在AC上 ， BD=DF； 说明：（1）CF=EB． （2）AB=AF+2EB． 【解答】 证明：（1）∵AD是∠BAC的平分线 ， DE⊥AB ， DC⊥AC ，∴DE=DC，∵ 在Rt△DCF和Rt△DEB中 ，，∴Rt△CDF≌Rt△EBD （HL）． ∴CF=EB ； （2）∵AD是∠BAC的平分线 ， DE⊥AB ， DC⊥AC ，∴CD=DE ． 在△ADC与△ADE中 ，∵ ∴△ADC≌△ADE （HL） ，∴AC=AE，∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB ． 【点评】 本题主要考查平分线的性质 ， 由已知能够注意到点D到AB的距离=点D到AC的距离 ， 即CD=DE ， 是解答本题的关键． 25．（2015秋?泰兴市校级月考）如图 ， 已知BE⊥AC ， CF⊥AB ， 垂足分别为E ， F ， BE ， CF相交于点D ， 若BD=CD．求证：AD平分∠BAC． 【考点】 角平分线的性质；全等三角形的性质；直角三角形全等的判定． 21 世纪教育网 【专题】 证明题． 【分析】 要证AD平分∠BAC ， 只需证DF=DE．可通过证△BDF≌△CDE（AAS）来实现． 根据已知条件 ， 利用AAS可直接证明△BDF≌△CDE ， 从而可得出AD平分∠BAC． 【解答】 证明：∵BE⊥AC ， CF⊥AB ，∴∠BFD=∠CED=90° ． 在△BDF与△CDE中 ，，∴△BDF≌△CDE （AAS）． ∴DF=DE，∴AD 是∠BAC的平分线． 【点评】 本题考查了全等三角形的判定和性质 ， 以及到角两边距离相等的点在角平分线上等知识．发现并利用△BDF≌△CDE是正确解答本题的关键． 26．（2014秋?芜湖校级期末）如图 ， 在△ABC中 ， AD是它的角平分线 ， 且BD=CD ， DE⊥AB、DF⊥AC ， 垂足为E、F ， 求证：EB=FC． 【考点】 角平分线的性质；全等三角形的判定与性质． 21 世纪教育网 【专题】 证明题． 【分析】 首先由角平分线的性质可得DE=DF ， 又有BD=CD ， 可证Rt△BED≌Rt△DFC（HL） ， 即可得出EB=FC． 21·cn·jy·com 【解答】 证明：∵AD是△ABC的角平分线 ， DE⊥AB、DF⊥AC ，∴DE=DF， ∠BED=∠CFD=90° ，在Rt△BED和Rt△DFC中 ，，∴Rt△BED≌Rt△CFD （HL） ，∴EB=FC ． 【点评】 此题主要考查角平分线的性质和全等三角形的判定和性质 ， 难度不大．27．（2014秋?陇西县期末）如图：E是∠AOB的平分线上一点 ， EC⊥OA ， ED⊥OB ， 垂足为C ， D． 求证：（1）OC=OD；（2）DF=CF． 【考点】 角平分线的性质；全等三角形的判定与性质；等腰三角形的判定与性质． 21 世纪教育网 【专题】 证明题． 【分析】 （1）首先根据角平分线的性质可得EC=DE ， ∠ECO=∠EDO=90° ， 然后证明Rt△COE≌Rt△DOE可得CO=DO； （2）证明COF≌△DOF可根据全等三角形的性质可得FC=FD． 【解答】 证明：（1）∵E是∠AOB的平分线上一点 ， EC⊥OA ， ED⊥OB ，∴EC=DE， ∠ECO=∠EDO=90° ，在Rt△COE和Rt△DOE中 ，，∴Rt△COE≌Rt△DOE （HL） ，∴CO=DO ； （2）∵EO平分∠AOB ，∴∠AOE=∠BOE，在△COF和△DOF中 ，，∴△COF≌△DOF （SAS） ，∴FC=FD ． 【点评】 此题主要考查了角平分线的性质 ， 以及全等三角形的判定与性质 ， 关键是掌握角平分线的性质：角的平分线上的点到角的两边的距离相等． 28．（2014秋?南昌期末）如图 ， AD是△ABC中∠BAC的角平分线 ， DE⊥AB于点E ， S△ABC=7 ， DE=2 ， AB=4 ， 求： （1）S△ACD； （2）AC的长． 【考点】 角平分线的性质． 网 【分析】 （1）根据S △ACD =S △ABC ﹣S △ABD， 利用三角形的面积公式可求解； （2）过点D作DF⊥AC于F ， 根据角平分线上的点到角的两边距离相等可得DE=DF ， 再根据（1）中所求S △ACD =3 列出方程求解即可． 【解答】 解：（1）S △ACD =S △ABC ﹣S △ABD =7 ﹣ ×4×2=3 ； （2）如图 ， 过点D作DF⊥AC于F ，∵AD 是△ABC中∠BAC的角平分线 ， DE⊥AB于点E ，∴DE=DF=2 ． ∵S △ACD =3，∴×AC×2=3，解得AC=3． 【点评】 本题考查了三角形的面积 ， 角平分线性质的应用 ， 注意：角平分线上的点到角的两边的距离相等． 29．（2014秋?苏州期末）一天 ， 数学老师布置一个思考题 ， 要求每个学习小组课后去讨论．你能和他们一起思考吗？题目是这样的： 如图 ， P是∠AOB的角平分线OC上一点 ， PD⊥OA ， PE⊥OB ， 垂足分别为D ， E． （1）比较PD与PE的长短 ， 得； （2）在OC上另取一点Q ， 画QF⊥OA ， QG⊥OB ， 垂足分别为F ， G．再比较QF、QG的长短 ， 得； （3）你可以在角平分线OC上再取其它一些点试试 ， 从中你发现了什么？ 【考点】 角平分线的性质． 21 世纪教育网 【分析】 （1）通过实际操作能得到P点到角的两边距离相等； （2）通过实际操作能得到P点到角的两边距离相等； （3）可以通过证明三角形全等来得到正确的结论； 【解答】 解：（1）用直尺量得PD=PE； （2）用直尺量得QF=QG； （3）证明：∵P是∠AOB的角平分线OC上一点 ，∴∠AOC=∠BOC，PD⊥OA， PE⊥OB ，∴∠ODP=∠OEP，∴△DOO≌△EPO，∴PD=PE，∴ 角平分线上的点到角的两边的距离相等． 【点评】 本题考查了角平分线的性质 ， 通过学生的动手、动脑使得学生更加牢固的掌握了新知识． 30．（2014秋?赣州期末）已知：如图 ， ∠B=∠C=90° ， M是BC的中点 ， DM平分∠ADC． （1）求证：AM平分∠BAD； （2）试说明线段DM与AM有怎样的位置关系？ （3）线段CD、AB、AD间有怎样的关系？直接写出结果．

推荐阅读


上一篇：效率|傻傻熬夜≠刻苦！提高晚上学习效率的7个妙招在这里

下一篇：校本|武冈市迎春亭新东中心小学：创新课堂促教研，落实“双减”促融合