浙江龙网

  1. 首页 > 生活百科 > >

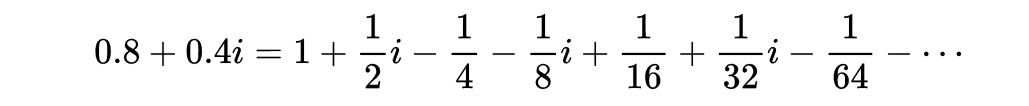
教师|用最简单的方式解释黎曼猜想（四），核心篇——非平凡零点与复变函数

教师数学


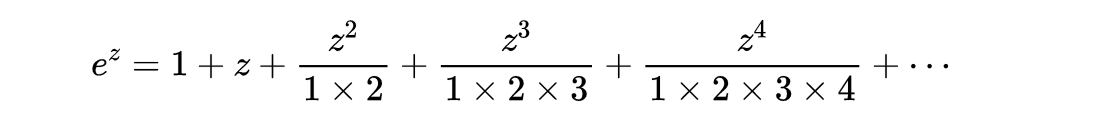
教师|用最简单的方式解释黎曼猜想（四），核心篇——非平凡零点与复变函数

文章图片


教师|用最简单的方式解释黎曼猜想（四），核心篇——非平凡零点与复变函数

文章图片


教师|用最简单的方式解释黎曼猜想（四），核心篇——非平凡零点与复变函数

文章图片


教师|用最简单的方式解释黎曼猜想（四），核心篇——非平凡零点与复变函数

文章图片


教师|用最简单的方式解释黎曼猜想（四），核心篇——非平凡零点与复变函数

文章图片


教师|用最简单的方式解释黎曼猜想（四），核心篇——非平凡零点与复变函数

文章图片


教师|用最简单的方式解释黎曼猜想（四），核心篇——非平凡零点与复变函数

文章图片


教师|用最简单的方式解释黎曼猜想（四），核心篇——非平凡零点与复变函数

文章图片


教师|用最简单的方式解释黎曼猜想（四），核心篇——非平凡零点与复变函数

文章图片


教师|用最简单的方式解释黎曼猜想（四），核心篇——非平凡零点与复变函数

文章图片



在上一篇文章 ， 我们已经讨论了黎曼zeta函数的一些零点 ， 每个负偶数都是zeta函数的零点：ζ(?2)= 0 ， ζ(?4)= 0 ， ζ(?6)= 0 ， 以此类推 。 这给我们提供了一种理解黎曼猜想的方法 ， 再次回顾下黎曼猜想的内容：


黎曼zeta函数的非平凡零点的实部都是1/2 。
但负偶数只是zeta函数的平凡零点 ， 我们不禁要问 ， 那些“非平凡零点”在哪里？为了回答这个问题 ， 我们必须走进复数世界 。

  • 数字系统 ， 维基百科
一个复数就是复平面上的一个点 ， 为了说明复平面 ， 我对复数做一点分析 ， 首先考虑我们之前讨论过的无穷级数：

  • x在-1到1之间
这适用于复数吗？是的（在某些条件下） 。 例如 ， 假设x是（1/2）i ， 那么级数收敛 。 事实上：

左边等于0.8+0.4i ， 右边可以利用i^2=-1来化简 ， 得到：

把右边表达式画在复平面上：

从实轴上的1开始 ， 加上1/2个虚单位（向上移动0.5） ， 再减去1/4（向左移动1/4）……最后得到一个螺旋图 ， 落在复数点0.8+0.4i处 。
回到非平凡零点 ， 我要告诉你的是 ， 黎曼zeta函数的非平凡零点都是复数！在1900年 ， 关于非平凡零的位置 ， 在数学上已经确定了如下事情：
  • 它们有无穷多个 ， 实部在0到1之间 。

阴影部分被称为临界带 ， 黎曼给出了更强的假设 ， 就是黎曼猜想——非平凡零点实部都落在1/2上（临界线上） 。
  • 零以共轭对的形式出现 。 也就是说 ， 如果a + bi是一个零点 ， 那么a - bi也是一个零点 。
  • 零点的实部关于临界线对称 。
把黎曼zeta函数定义域推广到复数范围?我们知道 ， 复数是普通实数的一个非常简单的扩展 ， 遵循所有的算术规则 ， 只是增加了i^2=-1 。 自然而然地 ， 我们可以用复数替代实数 ， 把函数的定义域扩展到整个复数范围 。 如

推荐阅读


上一篇：北京市|人力资源面试问题的三个方面

下一篇：建设|加快构建高质量教师教育体系