|热方程——数学物理学的基本方程之一，致使傅里叶级数的诞生

文章图片

文章图片

文章图片

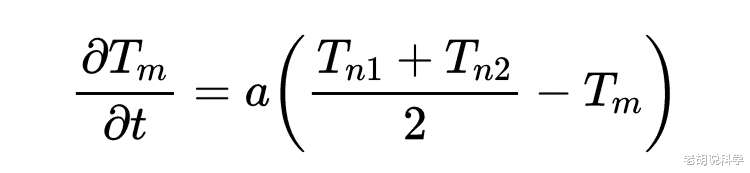
文章图片

文章图片

文章图片

文章图片

在数学物理学中，有三个基本方程：热、波和拉普拉斯方程。这三个方程都是含有偏导数的微分方程，在物理学和工程学中都有许多应用。但是，这些数学上的方程在直观上表达了什么？在这篇文章中，我们将深入探讨第一个方程，即热方程。
铁棒的问题假设有一根铁棒，我们知道热量在某一特定时间点是如何在铁棒上分布的，也就是说，我们知道它的每一个点的温度是多少。我们感兴趣的是以下问题：

热量分布将如何随时间变化？

正如我们在中学所学的，热量倾向于从温度较高的地方流向温度较低的地方传播。因此，我们实际上要做的是找到一个描述这一变化过程的方程式。当然，每当我们想模拟一个涉及 \"变化 \"的过程时，就会倾向于使用偏导数。
想象问题中的一维棒位于X轴上，那么描述其热分布如何随时间变化的微分方程如下：
其中α是一个比例常，而T=T(xt)是一个函数，提供了杆子上位于坐标 \"x \"的任何一点在时间 \"t \"上的温度。
现在，让我们试着用直觉、逻辑思维和一些基本的数学知识来推导它。
热方程的直观推导想象一下，我们只有少数几个点，而不是整个连续的铁棒，如下图所示。
Y轴代表每个点的温度。由于热量从较热的点流向较冷的点，那么每个点的温度变化将取决于其邻近点的温度。
让我们看一下上图中的粉红色点，它的两个“邻居”都有较低的温度，因此，当粉红色点开始冷却时，热量将被转移到这两个邻居。但是，如果它的一个邻居更热，另一个更冷，会发生什么？
那么，在这种情况下，将需要计算它们的平均温度。为了说明这一点，请看下图中的绿色点。
如果我们把绿色的中间点称为 \"M\" ，它的左邻N_1和右邻N_2 ，那么它们各自的温度将是T_8＝8 ， T_n1＝12 ， T_n2＝3.8 。绿色的邻居的平均温度为:
正如我们所看到的，蓝色点的平均温度小于其绿色对应点的温度。这意味着热量将从后者转移到前者身上，而绿点将被冷却一点。
我们如何概括这个想法并将其与导数的概念联系起来？
那么，我们在前面的例子中感兴趣的是下面这个量的符号：
如果这个差值大于0 ，那么中间点 \"M \"就会升温。差值越大，升温越快。因此，中间点升温的速度与上述差值成正比。为了在数学上表达这一点，我们这样写， M的温度相对于时间的导数等于这个差值乘以一个比例系数α 。
这已经类似于热方程了。让我们试着在右手边做一些数学上的运算，看看是否能发现什么：