【解析】

文章图片
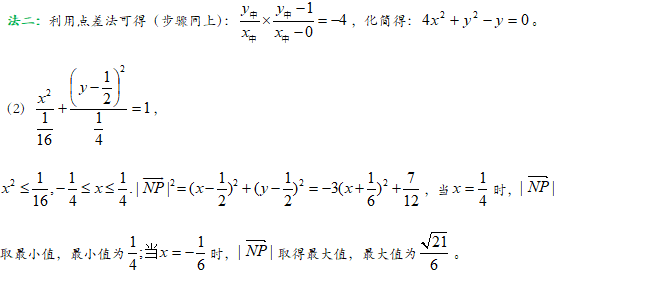
文章图片
【技巧二】抛物线中点弦问题 。
『秒杀策略』:抛物线:①。
简答题步骤规范模板:
方法一:
①设直线 的方程;
②直线与曲线联立 , 整理成关于 (或 )的一元二次方程;
③写出根与系数的关系;
④利用, 把根与系数的关系代入 。
方法二:点差法:
step1:设直线 与曲线 : 交于两点 、, 中点为, 则有 既在直线上又在曲线上 , 设 ,
Step2:代入点坐标:即,;
Step3:作差得出结论:(1)-(2)得: (作为公式记住 , 在小题中直接用 。 )
同理可推出其余三类方程的中点弦结论:
②。
③。
④。
【题型4】:求值(求k或p) 。
【答案】
【解析】
【答案】B
【解析】
【答案】2
【解析】
【答案】
【解析】
圆锥曲线的双切线问题处理技巧
【方法点拨】
这类试题主要的点在算理 , 即计算中如何合理的处理双切线 , 我总结如下:已知曲线外一点 ,向二次曲线 引两条切线, 设 .
第1步:分别写出切线的方程(注意斜率);
第2步:联立与曲线的方程 , 利用相切条件 , 得到代数关系① , ②式 , 从而以的 或 坐标为参数 , 进一步构造点横或纵坐标满足的同构方程方程③;
第3步:利用方程③根与系数的关系判断与曲线的位置关系 , 或完成其他问题.
【典例赏析】
(2021甲卷)已知抛物线 的顶点为坐标原点, 焦点在 轴上 , 直线 交 于 两点 , 且 .已知点, 且? 与 相切.
(1)求, ? 的方程;
(2)设 是 上的三个点 , 直线 均与? 相切 , 判断直线 与? 的位置关系 , 并说明理由.
【解析】
(1)设 的方程为,
由对称性可知 ,, 并假设点 在第一象限 , 点 在第四象限 ,
故直线 将代入抛物线方程解得:,
又因为, 故, 即
代入点 坐标可得:,
故 的方程为 .
再由直线 与? 相切可得? : .
(2)直线 与? 相切.
理由如下:
假设直线的斜率都存在 , 设,
则可得 的方程为:, 整理可得:,
由直线 与? 相切得:, 整理得: ①
同理: 的方程为,
由 与? 相切 , 即 ②.
由① , ②可知 分别是下列方程的两根 ,③.
若, 代入③式得:,
与是三个不重合的点矛盾 , 故,
则 , ④,
最后 , 由于 直线的方程为,
那么圆心 到直线 的距离为,
代入④式得: .
故直线 与? 相切.
当直线的斜率有一条不存在时 , 根据? 的位置关系可知 , 此时切线要么为, 要么为 .
不妨假设当 切线为 时 , 那么此时切线 为, 不合题意.
假设当 切线为 时 , 可取两点坐标为,
设切线 的方程为, 其与? 相切 , 故 ,得 .
即此时 , 切线, 过坐标原点与? 相切 , 即 .
这样: 的方程为:, 与 关于 轴对称 , 根据对称性可知 与? 相切 , 综上所述 , 直线 与? 相切.
变式1. (2020成都三诊).已知椭圆 : 的左焦点, 点 在椭圆 上.
(1)求椭圆 的标准方程;
(2)经过圆 : 上一动点 作椭圆 的两条切线 , 切点分别记为,, 直线,分别与圆 相交于异于点 的,两点.
推荐阅读
- 数学|称平行线能相交的数学奇才,遭质疑郁郁而终,其理论12年后被证实
- 教育部|终于轮到高中生“减负”了,教学进度将大幅调整,教育部已有通知
- 考试|高中生自创“汤圆”字体,风格可爱似元宝,老师看了忍不住夸赞!
- 申论|初中数学|实际问题与二次函数专题讲解+例题解析+专项训练,收藏
- 教师|教育部通知:禁止高中提前“结课”,同时教师也迎来“好消息”
- 高中物理|高中物理:电场、磁场解题宝典,建议收藏!
- 高中|高中九大学科思维导图最全汇总,高中三年都适用!(收藏)
- 疫情|疫情下,6个日夜,中山3名高中生“隔离”学习考试
- 高中生|韩调查:韩国中学生最想当老师
- 教师|2022考研数学是否为历年最难?难在哪里?










