(i)求证: ;
(ii)求 的面积的取值范围.
【解析】
(1)∵椭圆 的左焦点,
∴ .
将 代入, 得 .
又,
∴ .
∴椭圆的标准方程为 .
(2)(i)设点 .
①当直线,的斜率都存在时 ,
设过点 与椭圆 相切的直线方程为 .
由, 消去,
得 .
令, 整理得 .
设直线,的斜率分别为
∴ .
又, ∴ .
∴, 即为圆 的直径 ,
∴ .
②当直线 或 的斜率不存在时 ,
不妨设, 则直线 的方程为 .
∴,, 也满足 .
综上 , 有 .
(ii)设点 .
当直线 的斜率存在时 , 设直线 的方程为 .
由, 消去,
得
令, 整理得 .
则
∴直线 的方程为 .
化简可得, 即 .
经验证 , 当直线 的斜率不存在时 ,
直线 的方程为 或, 也满足 .
同理 , 可得直线 的方程为 .
∵ 在直线,上 , 即,.
∴直线 的方程为 .
由, 消去, 得 .
∴,.
又点 到直线 的距离 .
∴ .
令,.
则 .
又,
∴ 的面积的取值范围为 .
圆锥曲线选填压轴之距离
【方法点拨】
1.距离的几何意义:
(1)数轴上的距离: (终点减去起点的绝对值)
(2)平面内的距离: (构造直角三角形证明)
(3)三角形的边的关系:
2.距离的代数表达:
(1)点到点的距离公式:
(2)点到直接的距离公式:,
(3)两条平行线的距离公式: .
【基本方法】
1.几何转化法:充分利用代数表达式转化为几何意义;
2.坐标转化法:充分利用点和线段的坐标化 , 将几何图形问题转化为坐标运算问题;
3.构造函数法:恰当引入参数 , 建立函数关系 , 求解与距离相关的最值问题.
【典例赏析】
类型一直接利用距离转化

文章图片
【答案】A
【解析】
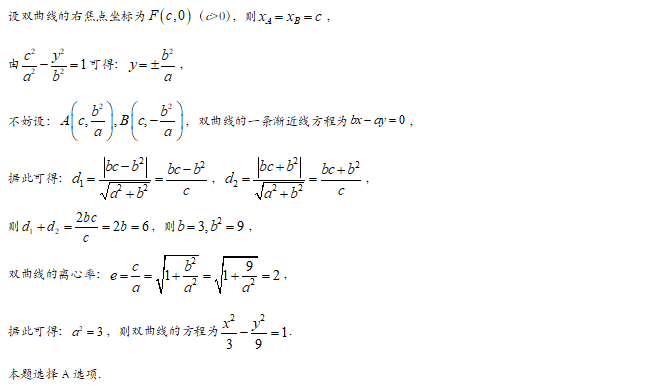
文章图片
【答案】B
【解析】
【答案】A
【解析】
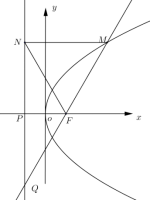
文章图片
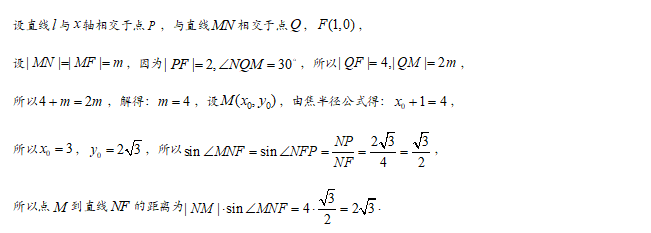
文章图片
【答案】B
【解析】
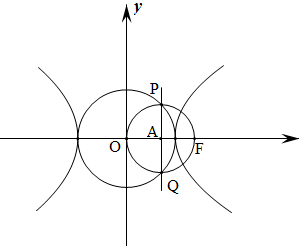
文章图片

文章图片
【答案】A
【解析】

文章图片
类型二将距离问题转化坐标运算
【答案】D
【解析】
【答案】B
【解析】

文章图片
【答案】C
【解析】

文章图片
【答案】B
【解析】
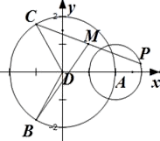
文章图片
推荐阅读
- 数学|称平行线能相交的数学奇才,遭质疑郁郁而终,其理论12年后被证实
- 教育部|终于轮到高中生“减负”了,教学进度将大幅调整,教育部已有通知
- 考试|高中生自创“汤圆”字体,风格可爱似元宝,老师看了忍不住夸赞!
- 申论|初中数学|实际问题与二次函数专题讲解+例题解析+专项训练,收藏
- 教师|教育部通知:禁止高中提前“结课”,同时教师也迎来“好消息”
- 高中物理|高中物理:电场、磁场解题宝典,建议收藏!
- 高中|高中九大学科思维导图最全汇总,高中三年都适用!(收藏)
- 疫情|疫情下,6个日夜,中山3名高中生“隔离”学习考试
- 高中生|韩调查:韩国中学生最想当老师
- 教师|2022考研数学是否为历年最难?难在哪里?










