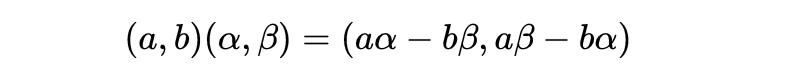
卓越|19世纪最伟大的发现是纯数学的性质大学

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

下面这个说法并不矛盾：我们越是偏重于理论方面，我们距离实际应用就越近。

19世纪的代数有两个看上去似乎针锋相对的特征。一个是越来越一般化、越来越抽象的趋势；另一个是专注于一些受约束的表达式，这些约束界定得比此前几个世纪更加小心谨慎。这种表面上的针锋相对，直接关系到19世纪的代数学家们提出并希望回答的问题在种类上的改变。
19世纪上半叶，代数学概念在英国的发展从根本上不同于欧洲大陆。阿贝尔、伽罗华及其他大陆数学家在致力于未解决问题并采用现有的成功方法时发展出了一些新概念。另一方面，跟阿贝尔和伽罗华同时代对代数学做出贡献的英国人，着手确立一种作为“论证科学”的代数学。自17世纪以来，数学家们就注意到，无论是高等分析学还是代数学，都没有达到我们在几何学中发现的那种严谨程度。
英国的代数学和函数的运算微积分?
剑桥分析学会从前的成员乔治·皮考克，拿出了第一部“旨在赋予代数学以论证科学品质”的重要作品。为了实现这个目标，皮考克提出了重估算术与代数之间的关系。算术没有被视为代数学的基础，而“只能被看作是一门‘暗示的科学’ ，让代数学的原理和运算适应于它，但既不被它所限制，也不被它所决定。 ”因此，皮考克把“算术”代数与“符号”代数分离开来。算术代数的基础是数，它的运算是算术运算。然而，符号代数是一门科学，仅仅依据确定的法则来看待标记与符号的结合，完全独立于符号本身的具体值。
布尔与逻辑代数
在三一学院的两位数学家哈密顿和凯莱发展两种新类型代数学的同时，一位基本上属于自学成才的英国人乔治·布尔发明了第三种、根本上完全不同的代数学。 1847年，布尔出版了一本篇幅不长的著作，题为《逻辑的数学分析》，德·摩根认为这本小书是划时代的作品。
逻辑学的历史可以用稍嫌简单的方式分为三个阶段：（1）希腊逻辑学，（2）经院逻辑学，（3）数理逻辑学。在第一阶段，逻辑表述由平常语言的词汇构成，服从于常规语法。在第二阶段，逻辑学开始以人工语言的使用为标志，在这样的语言中，单词和符号非常狭隘地限制了语义功能。在前两个阶段，逻辑学定理都源于平常的语言，而第三阶段的逻辑学则向完全相反的方式进行。尽管莱布尼茨有时候被视为后面这种观点的先驱，但它的全盛时期实际上应该是布尔的第一本著作，以及德·摩根的《形式逻辑》出版的那一年。特别是布尔的作品，强调了逻辑学应该与数学关联起来，而不是像苏格兰的威廉·汉密尔顿爵士所主张的那样，与形而上学联系在一起。